On the incidence of a subspace and some vertex of the unit cube

A new heuristic polynomial time algorithm has been implemented in Python. The algorithm rejects almost all subspaces of a sufficiently small dimension that are not incident to any vertex of the multidimensional unit cube [1, 2]. Of course, the worst-case computational complexity of the recognition problem is very hard.

The input is a matrix $L$ whose entries are coefficients of all linear forms $\ell_j$ in the system of equations $$\left\{\begin{array}{rcl} x_0&=&1\\ x_j&=&\ell_j(x_0,\dots,x_s), j>s\\ x_i&\in&\{0,1\}\\ \end{array}\right.$$ The output is equal to

False, when there exists a (0, 1)-solution, i.e., the subspace does not pass through any vertex;
True, when no obstacle is found.

Of course, True does not mean that a (0, 1)-solution exits.

Rows of the matrix $L$ correspond to linear forms $\ell_j$. For example, if there are two linear forms $\ell_2=2x_0+x_1$ and $\ell_3=3x_1$, then the matrix $L$ is equal to $$L=\left(\begin{array}{cc} 2&1\\ 0&3\\ \end{array}\right)$$ The matrix $L$ consists of variable coefficients of the system of equations.

Let us consider an example.

from fractions import Fraction

import numpy as np

from qualg import may_have_01solution

inputs = [
    np.array([[1, 1]]),
    np.array([[2, 1],
              [0, 3]]),
]
inputs.append(inputs[0] * 10**20)
inputs.append(inputs[1] * Fraction(1, 7))

for matrix_ell in inputs:
    print("Input:")
    print(matrix_ell)
    print("Result:")
    if may_have_01solution(matrix_ell):
        print("A (0,1)-solution *may* exist.")
    else:
        print("There is *no* (0,1)-solution.")
    print()

Implementation: `qualg.py`

from fractions import Fraction

import numpy as np


def may_have_01solution(matrix_ell):
    matrix_b = compose_b(matrix_ell)
    rank_a, rank_b = rank_ab(matrix_b)
    return rank_a != rank_b


def compose_b(matrix_ell):
    s = matrix_ell.shape[1] - 1
    n = matrix_ell.shape[0] + s
    height = (s + 1) * (s + 2) // 2
    dtype = matrix_ell.dtype
    matrix_b = np.zeros(shape=(height, n + 1), dtype=dtype)
    for i in range(s):
        matrix_b[i + 1, i] = -1
        matrix_b[(i + 1) * (2 * s - i + 2) // 2, i] = 1
    looo = np.array([1] + s * [0], dtype=dtype)
    triu_indices = np.triu_indices(s + 1)
    for j in range(n - s):
        matrix_q = matrix_ell[j] * (matrix_ell[j] - looo).reshape(-1, 1)
        matrix_q += np.tril(matrix_q, -1).T
        matrix_b[:, s + j] = matrix_q[triu_indices]
    matrix_b[0, -1] = 1
    return matrix_b


def rank_ab(matrix_b):
    matrix = matrix_b + Fraction()
    height, width = matrix.shape
    a_rank = b_rank = 0
    for column_index in range(width):
        if b_rank == height:
            break
        submatrix = matrix[b_rank:, column_index:]
        first_column = submatrix[:, 0]
        nonzero_indices = first_column.nonzero()[0]
        if nonzero_indices.size == 0:
            continue
        if first_column[0] == 0:
            first_nonzero = nonzero_indices[0]
            first_row_copy = submatrix[0].copy()
            submatrix[0] = submatrix[first_nonzero]
            submatrix[first_nonzero] = first_row_copy
        for row in range(1, height - b_rank):
            if first_column[row] != 0:
                ratio = first_column[row] / first_column[0]
                submatrix[row] -= ratio * submatrix[0]
        a_rank += column_index < width - 1
        b_rank += 1
    return a_rank, b_rank

The running time of the algorithm

There are illustrations that give an overview of the running time of the algorithm. Time was estimated using matrices $L$ with random integer entries uniformly distributed in the segment $[-10^9,10^9]$ (unless otherwise stated). The calculations were made using a personal computer (Core i5-3570 CPU, 16 GB of RAM).

The running time of the algorithm is almost completely determined by the time of exact calculation of the matrix rank.

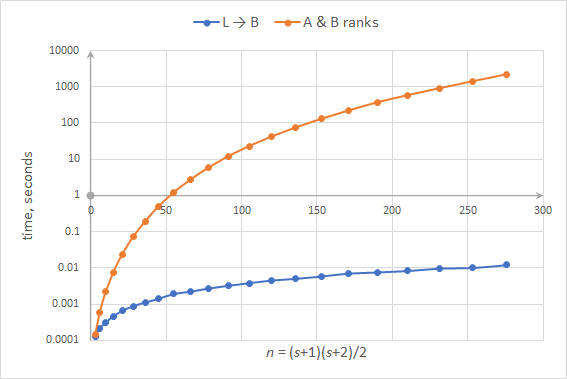
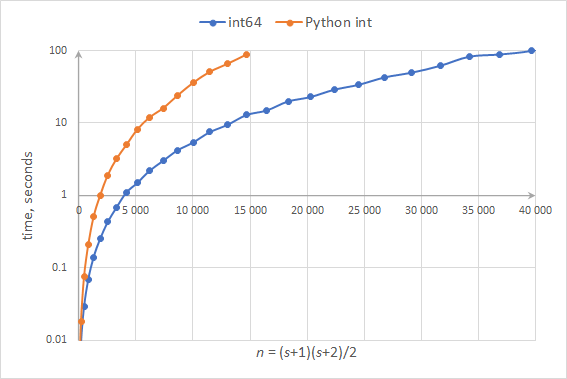
Both matrix preparation time and rank calculation time

The faster implementation to calculate the rank, the higher dimension of problems that can be solved.

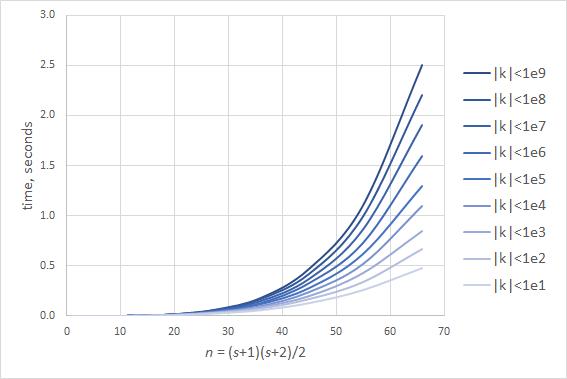
The matrix preparation time depending on the type of matrix entries

The running time of the algorithm essentially depends on the maximum absolute value of the matrix entries received as the input.

The running time depending on the maximum absolute value of entries

References

A.V. Seliverstov. Binary solutions to large systems of linear equations. Prikladnaya Diskretnaya Matematika, 2021, no. 52, pp. 5–15. (in Russian) DOI: 10.17223/20710410/52/1
O.A. Zverkov, A.V. Seliverstov. Effective lower bounds on the matrix rank and their applications. Programming and Computer Software, 2023, Vol. 49, No. 5, P. 441–447. DOI: 10.1134/S0361768823020160

On the incidence of a subspace and some vertex of the unit cube

Let us consider an example.

Implementation: qualg.py

The running time of the algorithm

References

Implementation: `qualg.py`